|
|
Subdivision algorithms | Solid subdivision algorithms | Multi-modal 3d reconstruction | Meshes | G-Spline surfaces |
Subdivision algorithms are a popular tool in CAD to design, create and model surfaces of arbitrary topological type. The initial input to a subdivision algorithm is an arbitrary net of control points. This net is refined to generate a finer control net. Iterating this process results in a sequence of ever finer nets that converges towards a limit surface of the desired topology and smoothness. Thereby the smoothness depends solely on the rules (subdivision masks) that have been used to compute the finer subdivided control nets. An example sequence of control nets for Loop's algorithm is shown below. To the left is the visualization of the Gaussian curvature of the limit surface.
|
 |
 |
 |
 |
It is possible to conclude
from the subdivision mask and the actual geometry of the
control net the curvature behavior of the limit surface at
the so-called extraordinary points. An example for Loop's
algorithm is shown below. Here some free parameters in the
construction of the subdivision algorithm have be used to
optimize the behavior of the limit surface.
This project aims at tailoring the subdivision rules in such a way that a desired geometrical behavior of the limit surface is guaranteed. Two examples of the results in this project are shown below.
This project aims at tailoring the subdivision rules in such a way that a desired geometrical behavior of the limit surface is guaranteed. Two examples of the results in this project are shown below.
 |
|
 |
|
Visualization
of
Gaussian
curvature
of
surfaces
from Loop's algorithm, from the modified
algorithm of Loop, from data dependent modified
algorithm of Loop using minimization of an
energy functional and from hybrid algorithm of
Loop (f.l.t.r.), see [PU00b].
|
Visualization
of
Gaussian
curvature
of
surfaces
from
a
modified
Catmull-Clark
algorithm to allow for arbitrary shapes, from an
optimized data-dependent Catmull-Clark algorithm
for arbitrary shapes, from an optimized
data-dependent Catmull-Clark algorithm for
elliptic shapes only (f.l.t.r.).The top row shows
the surface and the bottom row shows the
corresponding zoom at the extraordinary point. See
[GU07b]. |
Publications in this project can be found here: [GU08a], [GU08b], [GU07a], [GU07b], [GPU07], [GU06a], [GU06b], [GPU05], [Uml05], [Uml04], [PU01a], [PU00a], [PU00b], [Uml00], [PU98a], [PU98b].
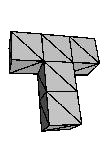
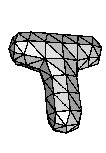
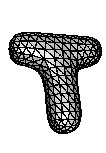
For surfaces subdivision algorithms are a well established tool for modeling and manipulation. For solid models subdivision techniques are a new research direction. Using subdivision schemes to model and manipulate solid models offers the versatility and flexibility of the subdivision approach. On the other hand the combinatorial complexity of the algorithms and models increases, which makes simulations for solid models computationally expensive.
The major focus in this research project is on efficient data representations and subdivision algorithms that allow to use the subdivision functions for the modeling as well as the simulation. Such an iso-geometric approach is particularly important for solid models, where the complexity is by nature much higher. To this end the subdivision rules need to be tailored for the physical process to be simulated, the simulation process, as well as the representation of the geometric model. So varioussolid subdivision schemes for tetrahedra or hexahedra with efficient integration strategies are developed.
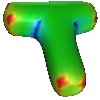
An example result is shown in the figure below. The shown mechanical part (left) is modeled with a Catmull-Clark algorithm for solid models and the simulations is computed based on Catmull-Clark elements. Here a radial force is applied to the cylindrical hole (left, green faces) while the model is fixed at the four drill holes at the bottom (left, red faces). The color in the middle and right figures visualizes the deformation stress (green = low stress, red = high stress). The right figure shows a cutaway view to the inside of the model. The advantages of this iso-geometric approach are a faster convergence and that conversions between the representations for the modeling and the simulation are obsolete.
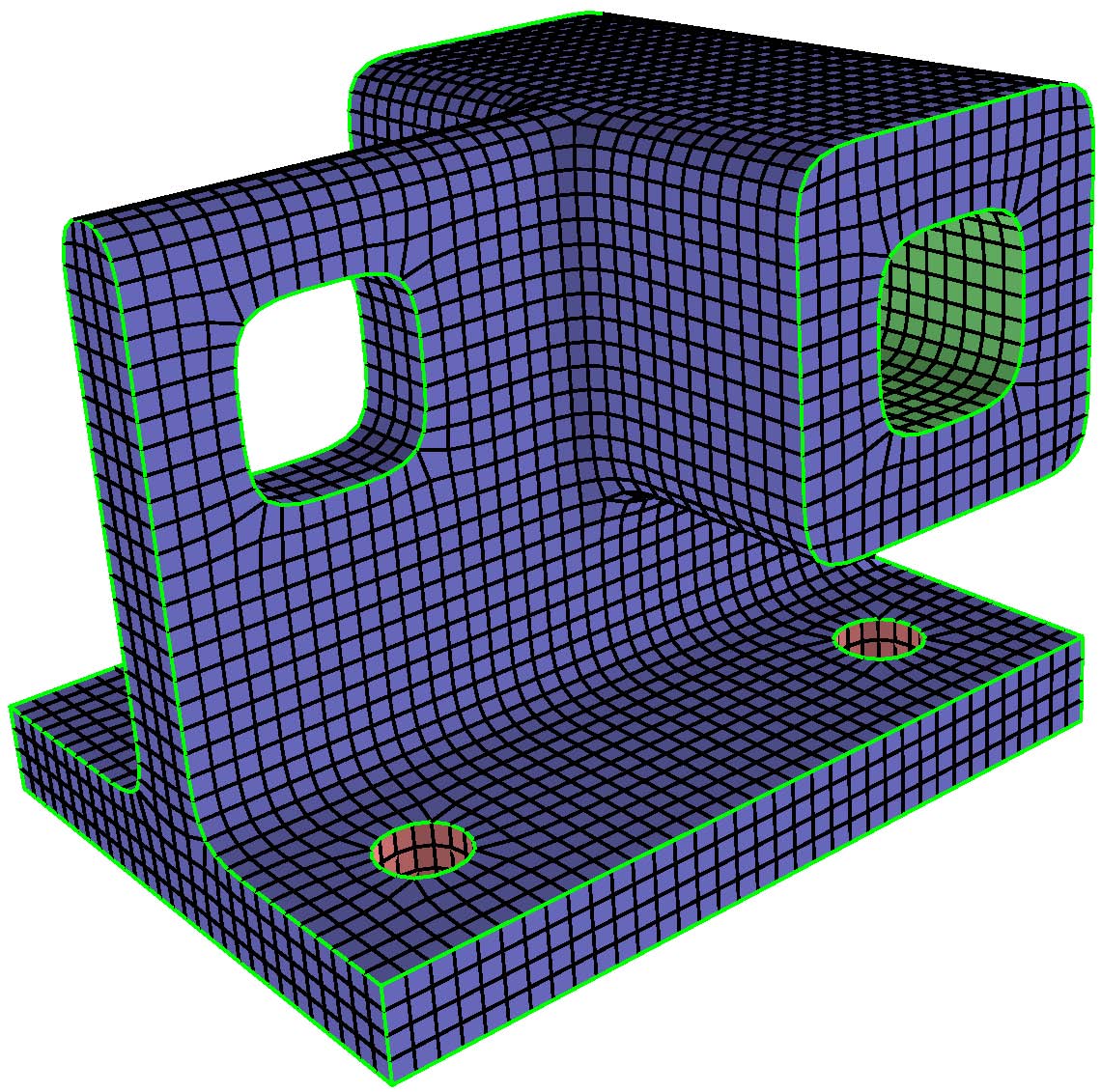 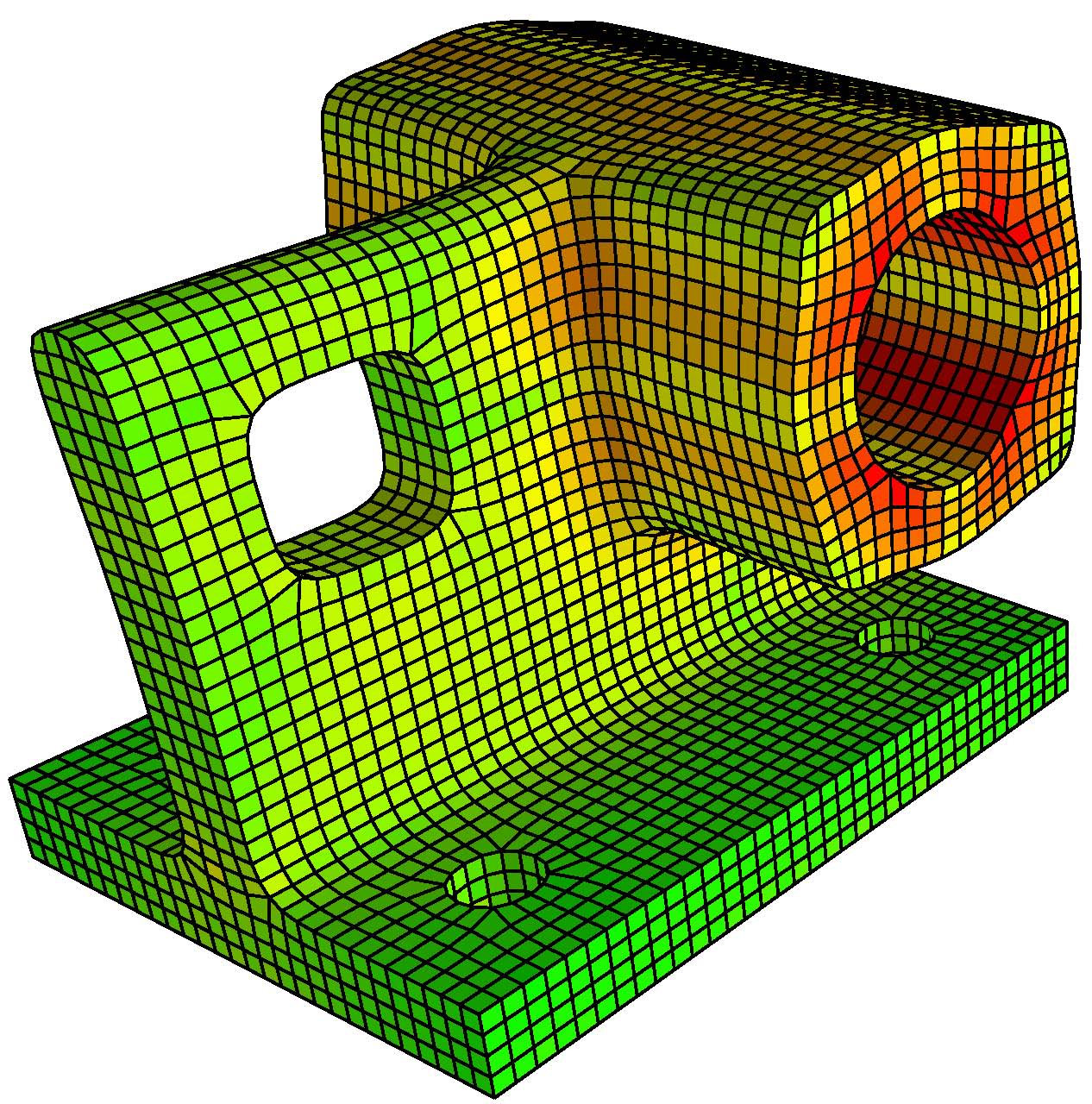 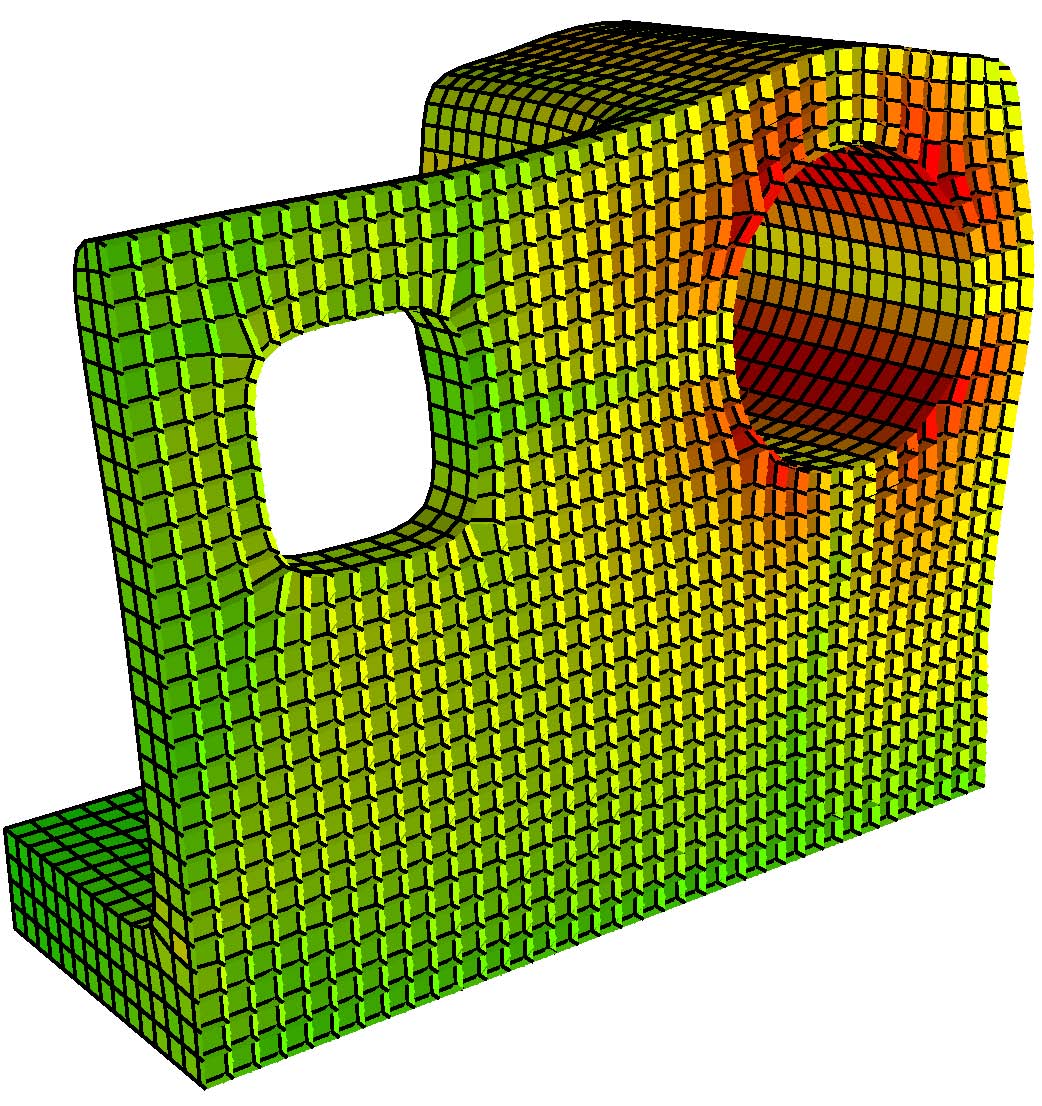 |
| Catmull-Clark solid (left) with stress visualization (middle and right) for a rotational force applied the cylindrical hole. See [BHU10a]. |
Publications in this project can be found here: [BHU11], [BHU10a], [BHU10b], [BHU10c], [LHU10].
Under construction!
 |
|
 |
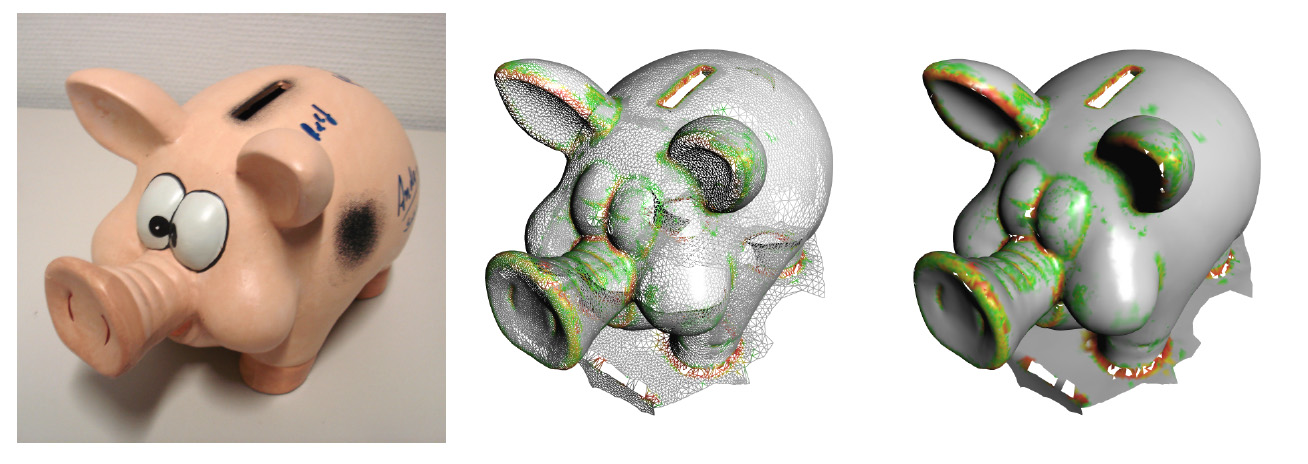
| A piggy bank reconstruction with a hand-hand laser scanner: original object (left), wire-frame (center), and smooth shaded triangulation with uncertainty visualization (right), see [DLU08]. | Face reconstructed from sterao matching from four camera system, see [DU11]. |
Publications in this project can be found here: [TLFU14], [CDFLU14], [DHRUH13], [BDFHU12], [CDDU12], [HDFU11], [DU11], [DU11a], [DLU10], [DLU08].
Manipulation and
transmission of large high dimensional scalar-, vector- or
tensor field data-set bears the problem of efficiently
processing this data. For this efficient data structures
supporting the necessary access and transmission
operations must be constructed. Based on well-known
representations for two-dimensional, meshed data
generalizations for different application areas are
designed and implemented. These include streaming data,
video data but also meshes and related data-structures
originating from FE simulation.
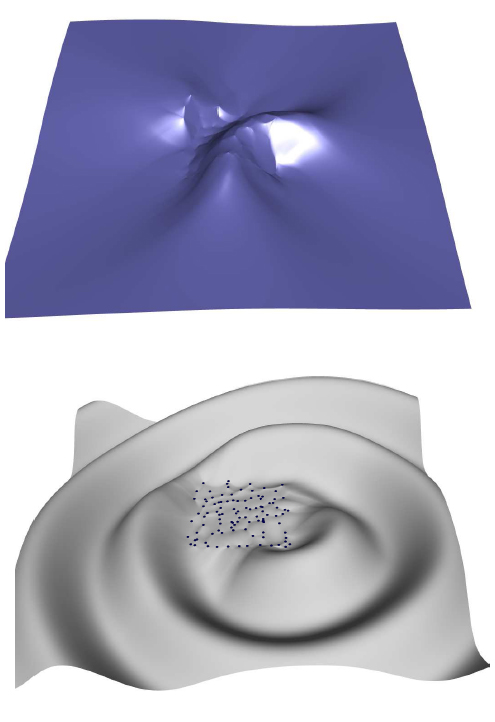
Two examples are shown in the figures below. To the left a method to extrapolate natural neighbor splines smoothly is shown. This scheme might be used in meshless FE simulations. To the right a data compression scheme for videos based on 3d triangulations is shown. Here, a video is represented as sequence in time (1d) of color images (2d) for which only the triangulation in 3d-space is stored.
Two examples are shown in the figures below. To the left a method to extrapolate natural neighbor splines smoothly is shown. This scheme might be used in meshless FE simulations. To the right a data compression scheme for videos based on 3d triangulations is shown. Here, a video is represented as sequence in time (1d) of color images (2d) for which only the triangulation in 3d-space is stored.
 |
|
 |
| Extrapolation of natural neighbor splines smoothly to the exterior of the domain using ghost points: extrapolated surface (blue, top), data points (blue, bottom) from a 2d cosine function and the error field (gray, bottom). See [BFHU09]. | Video compression by triangulating the time sequence of color image in 3-space. For the reconstruction linear interpolation is used. From left to right: original image, triangulation, reconstructed image. See [LUH08]. |
Publications in this project can be found here: [BCSU10], [LHU00], [BFHU09], [LUH08], [CSBFU08], [BU07a], [BU07b], [LHU07a], [LHU07b], [BBU06a], [BBU06b], [BU06], [LUHU06], [BU04].
G-Spline-Surfaces provide a means to model freeform surfaces. These surfaces consist of polynomial pieces with geometrically smooth transitions, i.e. the normals or curvatures are continuous. One way to construct such G2-surfaces for triangular nets (i.e. quartic box splines) is described in [PU99]. An example is shown below: to the left is the triangular control net of a generalized quartic box spline surface, in the middle the corresponding generalized quartic box spline surface and to the right the resulting G2-surfaces. The goal of this project is to generalize this approach to arbitrary smoothness order while keeping at the same time the number of the required patches to a minimum.
 |
 |
 |
| © Georg Umlauf | Last modified: 17.11.2014 |